AVL Tree

AVL Tree

AVL Tree adalah singkatan untuk Adelson-Velskii and Landis, AVL adalah bagian atau subtype dari Binary Search Tree (BST). Konsep AVL Tree adalah selisih dari height kiri dan kanan subtree tidak boleh lebih dari 1.

AVL tree harus selalu balance, sehingga setiap melakukan operasi akan di cek selisih height kiri dan kanan subtree jika lebih dari 1 maka disebut violation. Berikut adalah contoh dari violation, jika dilihat height dari subtree kiri 17 adalah 2 dan subtree kananya 0 maka selisihnya 2 ( violation ).

https://www.google.com/url?sa=i&url=http%3A%2F%2Fivansrarudiandi.blogspot.com%2F2016%2F05%2Favl-tree.html&psig=AOvVaw0u6xLhAVqqwO6eNKpO-PM4&ust=1588413552562000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCMih2u6zkukCFQAAAAAdAAAAABAE

AVL Tree Rotation

Seperti yang telah saya katakan bahwa setiap operasi kita perlu mengecek balance nya, jika tidak balance maka kita harus membuatnya balance dengan operasi rotation. Terdapat 2 jenis rotation, yaitu:

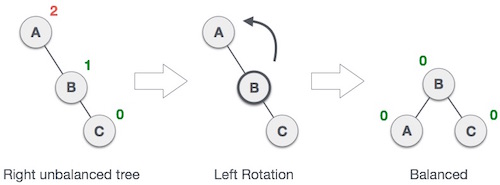
1. Single Rotation

Dalam single rotation terdapat dua jenis, jika violation terjadi pada subtree kanan maka left rotation, dan jika violation terjadi pada subtree kiri maka right rotation.

               

               

               

https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.freecodecamp.org%2Fnews%2Favl-tree-insertion-rotation-and-balance-factor%2F&psig=AOvVaw3qWvdkh1AfWWB2y28mvCAT&ust=1588413994177000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCNDNsK22kukCFQAAAAAdAAAAABAD

2. Double Rotation

Merupakan kombinasi dari single rotation, ketika case dimana violation pada subtree kiri memiliki anak kanan maka dilakukan operasi left right rotation dan sebaliknya pada right left rotation.

https://www.google.com/url?sa=i&url=https%3A%2F%2Fgithub.com%2Ftrekhleb%2Fjavascript-algorithms%2Ftree%2Fmaster%2Fsrc%2Fdata-structures%2Ftree%2Favl-tree&psig=AOvVaw38cHjVN8ZBFmpOEx3mmC8k&ust=1588414801715000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCMiKsLi4kukCFQAAAAAdAAAAABAD

AVL Tree Deletion

Deletion pada AVL tree sama dengan Binary Search Tree. Namun, setiap melakukan delete akan di cek balancenya agar tetap seimbang, jika tidak seimbang maka akan di lakukan rotation lagi.

Kesimpulan, AVL Tree berguna untuk case database dimana insertion dan deletion karena lebih cepat. Kebanyakan operasi BST menggunkan O(h) dimana h adalah height dari tree, sedangkan AVL tree pada worst case akan memakan waktu O(logn).  

- Febryan Stefanus Tandian - 2301942406