Heap & Tries

Heap

Heap adalah data structure tree yang terdiri dari 3 properti heap, yaitu:

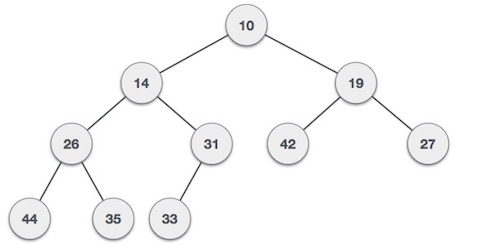
1. Min Heap: setiap node memiliki value yang lebih kecil dari childnya (value terkecil di root).

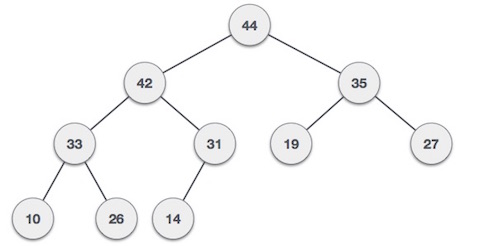
2. Max Heap: setiap node memiliki value yang lebih besar dari childnya (value terbesar di root).

3. Min-Max Heap: terdiri dari level dan setiap level memiliki heap yang berbeda.

Heap biasa direpresentasikan dalam bentuk array sehingga lebih mudah di digunakan. Index array pada heap dimulai dari 1, dan setiap melakukan insert akan dimasukkan ke index paling akhir. Untuk mengetahui index dari parent, left child, dan right child digunakan:

Parent(x) = x/ 2
left-child(x) = 2 * x
right-child(x) = 2 * x + 1

Min Heap

https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm

Max Heap

https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm

Min-Max Heap

https://www.google.com/url?sa=i&url=https%3A%2F%2Fstackoverflow.com%2Fquestions%2F14332279%2Fdelete-max-operation-in-a-min-max-heap&psig=AOvVaw3lQeJK5WhwlrqduIbAwNGx&ust=1589657768829000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCMj5y-fOtukCFQAAAAAdAAAAABAD

pada gambar diatas level 0 merupakan min, level 1 max, level 2 min, dan level 3 max. konsep nya sama, yaitu value terkecil berada pada heap min dan terbesar pada heap max.

Insertion

Pada insertion dilakukan mulai dari kiri ke kanan (diisi dari index yang terakhir). kemudian melakukan traverse dengan menukar valuenya, jika min heap maka value parent lebih kecil dari child nya dan sebaliknya pada max heap. 

contoh insertion pada min heap:

https://www.google.com/url?sa=i&url=http%3A%2F%2Fjuliusw.blog.binusian.org%2F2016%2F05%2F31%2Fdata-structures-pertemuan-8%2F&psig=AOvVaw2Fnh9b85mQDogPqf_SRDvx&ust=1589654721056000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCLDG7YHOtukCFQAAAAAdAAAAABAK

Deletion

Pada deletion key akan digantikan dengan value yang terakhir diinsert (index terakhir). lalu dilakukan traverse seperti pada insert.

contoh deletion pada min heap (delete key = 3):

https://www.google.com/url?sa=i&url=http%3A%2F%2Fjuliusw.blog.binusian.org%2F2016%2F05%2F31%2Fdata-structures-pertemuan-8%2F&psig=AOvVaw2Fnh9b85mQDogPqf_SRDvx&ust=1589654721056000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCLDG7YHOtukCFQAAAAAdAAAAABAD

Aaplikasi dari heap adalah heap sort dan Djikstra algorithm.

Tries

Tries atau prefix tree adalah data stucture tree yang digunakan untuk menyimpan string yang berurut (dalam karakter).

https://www.google.com/url?sa=i&url=http%3A%2F%2Fbtechsmartclass.com%2Fdata_structures%2Ftries.html&psig=AOvVaw0OXg-WKXADeNoAkp4NY1IY&ust=1589657518758000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCKjvsvDNtukCFQAAAAAdAAAAABAD

Implementasi dari tries misalnya pada auto complete web browser, keyboard smartphone, word bubble, dan lain-lain. Dari suatu karakter kita bisa mendapatkan string yang diingkan, misalnya pada contoh diatas jika kita memasukkan karakter B maka akan memunculkan Ball, Bat, dan Be.